Raspberry Pi メモ (13) OpenGL ES2(6)

OpenGL ES2(6) シェーダで照明 (2012/10/19, 2017/12/24)

これまでのサンプルでは照明の効果を組み込んでいなかったので、三角形がどんな角度でも常に同じ明るさで表示されていました。実世界の物体は光の当たり方で明るい部分と暗い部分があるのが普通です。さらに、なめらかな表面では光が反射します。今回はこういった照明の効果をシェーダ (GLSL) で実装する事にします。光源が１つの場合の Phong の反射モデル (フォンシェーディング) をシェーダで計算することで、画面に表示されるすべてのピクセル毎に細かく計算してリアルな画像を表示できるようにします。物体を構成するすべての面に関して、ピクセル毎に処理を行う場合、 シェーダの威力が非常に大きく発揮 されます。

Raspberry Pi (ラズベリーパイ) が使っている ARMv6(700MHz) のようにいまいち非力な CPU を使っていても GPU (VideoCore4) のおかげでリアルタイムに処理できます。 35ドルという値段もすごいですが、全体の消費電力が 3W のコンピュータでリアルタイムのフォンシェーディングを実現できることは驚きです。

フォンシェーディング (Phong shading)

光が光源から出て、色々なものに反射することで、すべての方向から照らされた物体の表面の色を計算で求めるのは非常に大変そうです。コンピュータで照明を扱うためにはある程度の簡略化 (モデル化) が必要です。物体を照らす光の計算は次の３つに分解して計算し、最後に適当な割合で合計すると簡単な計算でそれらしく表示する事が出来ます。

（環境光の色ｘ環境光の強度）＋（拡散光の色ｘ拡散光の強度）＋（反射光の色ｘ反射光の強度）

環境光 (ambient light)

直接光源から来る光に照らされるのではなく、周囲（環境）にある光です｡実際はどんな光もなんらかの光源からやってきて、いろいろな反射や拡散の結果として存在する光ですが、細かく区別できない光を一様の環境光 (ambient light) として表します。曇りの日には環境光は強く、宇宙空間では非常に弱くなります。これまでのサンプルは環境光だけで照明されているとも言うこともできます。

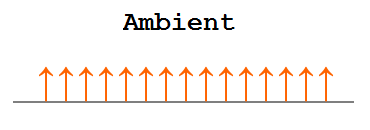
拡散光 (diffuse light)

光に照らされた物体の表面は、どこから見ても光が強いほど明るく見えます。これは光に照らされた表面からすべての方向に反射 (拡散) する光があることを示します。これを拡散光 (diffuse light) と呼びます。表面を照らす光の強さは、光の方向に垂直な面が最も単位面積あたりの光が強く、傾いた面は弱くなります。正午の太陽の光より、夕方の光が弱くなるのと同じです。物体の表面に対する入射光の垂直成分の大きさに比例します。

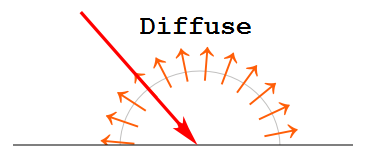
鏡面反射光 (specular light)

スペキュラ (specular) またはハイライト (hightlight) とも呼びますが、鏡面反射の意味です。なめらかな面に入射した光の一部は鏡に反射するように進みます。入射光の角度によって反射する光の方向と強さは変化します。表面の性質となめらかさの程度によって、金属面のように一方向だけに強く反射する場合と、プラスチックのように鈍く弱く反射する場合があります。

実際の計算

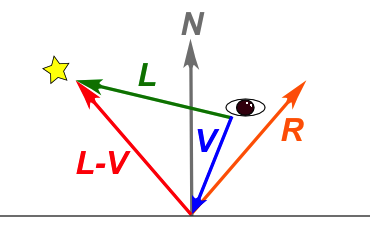
物体の色や照明は最終的にスクリーンに表示される点(ピクセル)の色として表されます。このような個々のピクセルに対応する物体表面の点の座標をベクトル V で表すことにします。また、点光源の座標をベクトル L で表すことにすると、物体表面の点から光源に向かう入射光ベクトルはベクトルの減算 L - V で表せます。視点が原点 (視点座標系までバーテックスシェーダで変換済みのため) にある場合、注視している表面上の点から視点に向かう視線ベクトルは -V となります。

面の法線ベクトル N と入射光ベクトル L - V はどちらも長さ1に正規化されている場合、cos θ は N と L - V の内積で求められます。したがって、それぞれ正規化した法線ベクトルと入射光ベクトルの内積 dot(N , L - V) が拡散光の強度となります。反射光の強度は、面から視点に向かう視線ベクトル -V と反射光ベクトル R の角度 φ の関数となり、角度が大きくなるにつれて1.0から急速に小さくなれば、特定の角度前後でキラリと光ることで反射光を「それらしく」表現できます。この関数として cos φ を使うと、それぞれ正規化した視線ベクトルと反射光ベクトルの内積として容易に求められ、φが0付近で値が 1.0 近くになります。そのままではゆっくりとしか変化しないので cos φ を 40乗したものを反射光強度を求める関数として使います。この辺はいい加減なようですが、「それらしく」表示できればいいので適当に決めます。「40乗」の部分は表現したい材質によって変更します。

下の図は今回のサンプルを実行した時の4枚の連続したスクリーンショットです。左上と右下の明るさの違いは三角形の面と上後方の光源 (0, 60, 60) との角度で拡散光の強度が異なることを示しています。右上の三角形は頂点のない中央部分が反射光で明るくなっていますが、シェーダを使ってピクセル毎に照明の計算を行なっていることが分かります。法線ベクトルが頂点間のピクセル毎で補間されて、ピクセル毎に反射光の方向がわずかに異なるため、点光源が1枚の平面を照らしている状況が再現できています。

前回のサンプルと比べて、光の効果をちゃんと扱うと三角形1枚でも格段に見映えが良くなります。

バーテックスシェーダ

今回はメモ(11) のサンプルで使ったバーテックスシェーダに渡した投影変換行列とビュー行列の積 uVpMatrix (M_proj M_eye) とワールド座標系への変換行列と回転行列の積 uModelMatrix (M_world M_rotate ) とは異なる形で行列を渡すことにします。

今回は座標変換に使う行列の呼び方を OpenGL 流に次の表のように変更します。

投影変換行列 (2次元変換)	M_proj
ワールド座標系から視点座標系への変換行列	M_view
ローカルからワールド座標系への変換行列	M_model
ローカルの頂点を回転させる行列	M_rotate
ローカルの頂点から座標系への変換行列	M_modelview

頂点座標の変換の式は次のようになります。

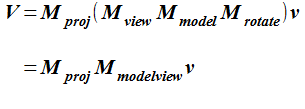
今回のシェーダでは平面の法線ベクトルを使います。回転する物体の頂点を視点から見えるシーンとなるように座標変換するのと同じように、視点から見える法線ベクトルの方向を変換する必要があります。このためには法線ベクトル専用の「inverse transpose」した変換行列が必要となります。この逆行列の転置行列は拡大縮小の無い純粋な回転行列では、元の行列と等しくなるため、頂点の変換行列 (uMVMatrix) の平行移動成分を0にしたものと法線ベクトルの変換行列 (uNormalMatrix) は同じになります。

attribute vec3 aPosition;
attribute vec3 aNormal;
attribute vec2 aTexCoord;

varying   vec3 vPosition;
varying   vec3 vNormal;
varying   vec2 vTexCoord;

uniform   mat4 uProjMatrix;   // 投影行列
uniform   mat4 uMVMatrix;     // モデルビュー行列
uniform   mat4 uNormalMatrix; // 法線行列

void main(void) {
  // 頂点座標を2次元に変換して出力
  gl_Position = uProjMatrix * uMVMatrix * vec4(aPosition, 1.0);

  // テクスチャ座標はそのまま出力
  vTexCoord = aTexCoord;

  // 頂点座標を視点座標系に変換して出力
  vPosition = vec3(uMVMatrix * vec4(aPosition, 1.0));

  // 法線ベクトルを視点座標系に変換して出力
  vNormal = vec3(uNormalMatrix * vec4(aNormal, 1));
}

フラグメントシェーダ

今回の主役はフラグメントシェーダです。照明関連の計算処理は1ピクセル毎に行うので、フラグメントシェーダがすべて担当します。このフラグメントシェーダは多機能になっていて、ユニフォーム変数に設定する値で動作を指定します。

変数名	内容
uTexFlag	テクスチャを使わない場合は 0
uEmit	発光しない場合は 0
uAmb	環境光強度 (0.0 - 1.0)
uSpec	反射光強度 (0.0 - 1.0)
uLightPos.xyz	点光源なら光源位置、平行光源なら入射光ベクトル
uLightPos.w	0.0なら平行光源、それ以外は点光源
uColor.rgb	面の色を指定
uColor.a	テクスチャと混合する面指定色の割合

上の計算内容の解説とコード中のコメントを比べながらコードを追ってみてください。このシェーダプログラムが1ピクセル毎に走ります。

precision mediump float;

varying vec3   vPosition;
varying vec3   vNormal;
varying vec2   vTexCoord;
uniform sampler2D uTexture;
uniform int    uTexFlag;
uniform int    uEmit;
uniform float  uAmb;
uniform float  uSpec;
uniform vec4   uLightPos;
uniform vec4   uColor;

void main(void) {
  vec4 color;
  vec3 lit_vec;
  float diff;
  float Ispec;

  // 反射光の色(白)を変数に代入
  vec4 white = vec4(1.0, 1.0, 1.0, 1.0);

  // 面の法線ベクトル(N)を正規化
  vec3 nnormal = normalize(vNormal);

  // uLightPos.w を光源の切り替えに使用
  if (uLightPos.w!=0.0) {
    // 点光源の場合、入射光 (L-V) 
    lit_vec = normalize(uLightPos.xyz - vPosition);
  } else {
    // 平行光源
    lit_vec = normalize(uLightPos.xyz);
  }

  // 面から視点に向かう視線ベクトル (-V) 
  vec3 eye_vec = normalize(-vPosition);

  // 反射光ベクトル (R) を求める
  vec3 ref_vec = normalize(reflect(-lit_vec, nnormal));

  // 拡散光と反射光強度
  if (uEmit == 0) {
    // 拡散光強度を求める
    diff = max(dot(nnormal, lit_vec), 0.0) * (1.0 - uAmb);
    // 反射光強度を求める
    Ispec = uSpec * pow(max(dot(ref_vec, eye_vec), 0.0), 40.0);
  } else {
    // 自ら発光する場合は照明の影響を受けない 
    diff = 1.0 - uAmb;
    Ispec = 0.0;
  }

  if (uTexFlag != 0) {
    // テクスチャと面の指定色の混合
    color = uColor * texture2D(uTexture, vec2(vTexCoord.s, vTexCoord.t));
    color = mix(diff * uColor, color, uColor.w);
  } else {
    // テクスチャを使わない場合は面の指定色
    color = uColor;
  }

  // 環境光、拡散光、反射光の加算混合
  gl_FragColor = vec4(color.rgb * (uAmb+diff) + white.rgb * Ispec,1);
};

シェーダ用パラメータ

シェーダ用の各種設定を構造体にまとめて管理します。主にシェーダ内の変数の位置の記録です。

typedef struct {
  GLint uProjMatrix;   // 投影行列の位置
  GLint uMVMatrix;     // モデルビュー行列の位置
  GLint uNormalMatrix; // 法線行列の位置
  GLint uTexture;      // テクスチャの位置
  GLint uTexFlag;      // テクスチャの使用フラグの位置
  GLint uEmit;         // 面は発光フラグの位置
  GLint uAmb;          // 環境光強度の位置
  GLint uSpec;         // 反射光強度の位置
  GLint uLightPos;     // 光源の位置
  GLint uColor;        // 面の色
  GLint aPosition;     // 頂点座標配列の位置
  GLint aNormal;       // 法線ベクトル配列の位置
  GLint aTexCoord;     // テクスチャ座標配列の位置
  Mat4  projMat;       // 投影行列
  GLint textureFlag;   // テクスチャの使用フラグ
} ShaderParams;

シェーダ用パラメータの初期化用の関数

シェーダを使う前にシェーダ用の構造体 (ShaderParams) にシェーダ内の変数の位置を記録しておきます。

void initShaderParameter(ShaderParams *sp, GLuint prog)
{
  // 行列のユニフォーム変数位置を取得
  sp->uProjMatrix = glGetUniformLocation(prog, "uProjMatrix");
  sp->uMVMatrix = glGetUniformLocation(prog, "uMVMatrix");
  sp->uNormalMatrix = glGetUniformLocation(prog, "uNormalMatrix");

  sp->uTexture  = glGetUniformLocation(prog, "uTexture");
  sp->uTexFlag  = glGetUniformLocation(prog, "uTexFlag");
  sp->uEmit     = glGetUniformLocation(prog, "uEmit");
  sp->uAmb      = glGetUniformLocation(prog, "uAmb");
  sp->uSpec     = glGetUniformLocation(prog, "uSpec");
  sp->uLightPos = glGetUniformLocation(prog, "uLightPos");
  sp->uColor    = glGetUniformLocation(prog, "uColor");

  // アトリビュートの変数位置を取得
  sp->aPosition = glGetAttribLocation(prog, "aPosition");
  sp->aNormal   = glGetAttribLocation(prog, "aNormal");
  sp->aTexCoord = glGetAttribLocation(prog, "aTexCoord");
}

パラメータ設定用のラッパー関数

シェーダに対して glUniform で各種の値を設定しますが、使い易くするためのラッパー関数 (wrapper function) です。

// 光源位置、光源種類
void setLightPosition(ShaderParams *sp, GLfloat x, GLfloat y, GLfloat z, GLfloat type)
{
  glUniform4f(sp->uLightPos, x, y, z, type);
}

// テクスチャ使用：使用しない [0]
void useTexture(ShaderParams *sp, GLint flag)
{
  glUniform1i(sp->uTexFlag, flag);
  sp->textureFlag = flag;
}

// 発光 : 発光しない [0]
void setEmissive(ShaderParams *sp, GLint flag)
{
  glUniform1i(sp->uEmit, flag);
}

// 環境光強度 (0.0 - 1.0) [0.3]
void setAmbientLight(ShaderParams *sp, GLfloat intensity)
{
  glUniform1f(sp->uAmb, intensity);
}

// スペキュラ強度 (0.0 - 1.0) [0.5]
void setSpecular(ShaderParams *sp, GLfloat intensity)
{
  glUniform1f(sp->uSpec, intensity);
}

// 物体の色、テクスチャ不透明度 [1,1,1,1]
void setColor(ShaderParams *sp, GLfloat r, GLfloat g, GLfloat b, GLfloat a)
{
  glUniform4f(sp->uColor, r, g, b, a);
}

main

以下のコードは main 関数全体です。前回からの違いは赤で示しています。シェーダ用のパラメータが増えている部分が大きな違いです。

このサンプルではテクスチャの裏側が表示されないように三角形を2枚張り合わせています。頂点1つに対して法線ベクトルは1つしか設定できないため、表用の頂点と裏用の頂点で頂点座標は同じでもテクスチャ座標と法線ベクトルが異なる２つの頂点を使っています。貼り合わせることで隠れてしまう面の裏側を背面消去(glCullFace(GL_BACK)) しています。「背面消去」は「裏側から見ると面が透明」に見えるようにすることです。内部処理では面の裏側が正面を向く場合は「全く処理をしない＝面を無いのものとして扱う」ことで処理の負荷を半減する手法です。面が裏か表かを判断するために「頂点が反時計回りなら正面＝glFrontFace(GL_CCW)」と決めています。

int main ( int argc, char *argv[] )
{
  unsigned int frames = 0;
  int   res;
  Mat4  viewMat;
  Mat4  rotMat;
  Mat4  modelMat;
  Mat4  normalMat;
  Mat4  modelView;
  float aspect;
  int   size;

  bcm_host_init();
  res = WinCreate(&g_sc);
  if (!res) return 0;
  res = SurfaceCreate(&g_sc);
  if (!res) return 0;
  res = InitShaders(&g_program, vShaderSrc, fShaderSrc);
  if (!res) return 0;

  createBuffer();

  size = LoadFile("num256.bmp", (void *)g_bmpbuffer);
  printf("LoadFile %d \n", size);
  bmpCheck(&g_tt, (void *)&g_bmpbuffer);
  makeTexture(&g_tt, 255);
  createTexture(&g_tt);

  glUseProgram(g_program);
  // シェーダ用のパラメータを設定
  initShaderParameter(&g_sp, g_program);
  // シェーダ用のラッパー関数の実行
  setLightPosition(&g_sp, 0, 800, 600, 1);
  useTexture(&g_sp, 1);
  setColor(&g_sp, 0.5, 0.5, 1.0, 1.0);
  setEmissive(&g_sp, 0);
  setAmbientLight(&g_sp, 0.4);
  setSpecular(&g_sp, 0.7);

  // 投影行列の設定
  aspect = (float)g_sc.width / (float)g_sc.height;
  setProjectionMatrix(&g_sp, 1, 1000, 53, aspect);

  // モデルビュー行列の作成
  makeUnit(&viewMat);
  setPosition(&viewMat, 0, 0, -2);
  makeUnit(&modelMat);
  mulMatrix(&modelView, &viewMat, &modelMat);

  makeUnit(&rotMat);
  setRotationX(&rotMat, 2.0);

  // 背面消去の設定
  glCullFace(GL_BACK);
  glFrontFace(GL_CCW);
  glEnable(GL_CULL_FACE);

  glEnable(GL_DEPTH_TEST);
  glClearColor(0.1f, 0.2f, 0.6f, 1.0f);

  /* 1200frame / 60fps = 20sec */
  while(frames < 1200) {
    glViewport(0, 0, g_sc.width, g_sc.height);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    // モデルビュー行列を回転
    mulMatrix(&modelView, &modelView, &rotMat);
    // 法線行列を作成(modelView の回転成分 = modelMat)
    copyMatrix(&normalMat, &modelView);
    setPosition(&normalMat, 0, 0, 0);

    // シェーダにモデルビュー行列を設定
    glUniformMatrix4fv(g_sp.uMVMatrix, 1, GL_FALSE, modelView.m);
    // シェーダに法線行列を設定
    glUniformMatrix4fv(g_sp.uNormalMatrix, 1, GL_FALSE, normalMat.m);

    Draw();
    eglSwapBuffers(g_sc.display, g_sc.surface);
    frames++;
  }
  return 0;
}

ソースのダウンロードと使い方

点光源で照らされた三角形が X軸まわりに回転するだけのサンプルのソースです。

Jessie 以前向け: triangel04.tar.gz (18KB)
Raspbian Stretch 向け: triangel04a.tar.gz (20KB) (2017/12/24)

triangle.c が今回のソース全体、triangle はコンパイルした実行ファイル、build はコンパイル用のシェルスクリプトです。

jun@raspberrypi ~/triangle04a $ ls -lt
-rwxr-xr-x 1 pi pi    211 Dec  7 16:10 build
-rw-r--r-- 1 pi pi 131126 Oct 30  2008 num256.bmp
-rwxr-xr-x 1 pi pi  24472 Dec  7 16:16 triangle
-rw-r--r-- 1 pi pi  18936 Dec  7 16:16 triangle.c

公式OSの Raspbian の場合、pi ユーザ(または video グループ権限を持つユーザ) で以下のようにファイルを解凍して、コンパイル、実行できます。20秒間動作して終了します。

$ tar zxf triangle04a.tar.gz
$ cd triangle04a
$ ./build
$ ./triangle

これまでの解説でOpenGL ES2を使った3次元グラフィックスはほとんどカバーできるのではないかと思います。 OpenGL ES2関連ではパーティクルや影、文字の表示など説明していない部分もありますが、直接 OpenGL ES2 には関係しない部分である「多くの物体の形状のデータの作成方法」、「多くの物体の形状、動き、速度の管理」といったアプリケーションの内容に依存する部分が実は難しいところです。 OpenGL ES2 の解説はこれで一段落です。

Raspberry Pi(ラズベリーパイ) メモ (13)

OpenGL ES2(6) シェーダで照明 (2012/10/19, 2017/12/24)

フォンシェーディング (Phong shading)

環境光 (ambient light)

拡散光 (diffuse light)

鏡面反射光 (specular light)

実際の計算

バーテックスシェーダ

フラグメントシェーダ

シェーダ用パラメータ

シェーダ用パラメータの初期化用の関数

パラメータ設定用のラッパー関数

main

ソースのダウンロードと使い方

続く...

Jun's Homepage

ラズベリーパイメモ

ARM アセンブリ

Raspberry Pi(ラズベリーパイ) メモ (13)

OpenGL ES2(6) シェーダで照明 (2012/10/19, 2017/12/24)

フォンシェーディング (Phong shading)

環境光 (ambient light)

拡散光 (diffuse light)

鏡面反射光 (specular light)

実際の計算

バーテックスシェーダ

フラグメントシェーダ

シェーダ用パラメータ

シェーダ用パラメータの初期化用の関数

パラメータ設定用のラッパー関数

main

ソースのダウンロードと使い方

続く...

Jun's Homepage

ラズベリーパイ メモ

ARM アセンブリ

ラズベリーパイメモ