OpenGL ES2(4) - 三次元で三角形 (2012/10/06, 2017/12/24)
前回はRaspberry Pi 上で OpenGLES2 を使って 2次元の三角形を移動するだけのシェーダを紹介しました。 今回は3次元の回転に挑戦します。 複数の物体が動きまわり、さらにカメラも動くような 3次元のコンピュータグラフィック はどのように計算するのでしょうか。 今回は数式が出てきますが、 計算自体はコンピュータがやってくれるので、使い方のパターンを習得すれば大丈夫です。
今回もちょっと長いので簡単な目次です。
- 3次元グラフィックスと行列
- 行列とベクトルの乗算
- 平行移動と回転
- 行列同士の乗算
- モデルビュー行列と透視投影変換行列
- 頂点シェーダにおける座標変換
- 透視投影変換行列
- サンプルコード
- ソースのダウンロードと使い方
3次元グラフィックスと行列
3次元のコンピュータグラフィックスでは表示する物体の形状や位置を3次元の座標値 (x,y, z) で表します。 表示する物体の数や形状の複雑さに依存して、数十から数万の座標を扱うことになります。 例えばボクシングをしている場面を想像して下さい。 ボクシンググローブは選手がパンチを繰り出しても、足を使って移動しても位置が変わります。 二人の選手が独立に動いている場合の4つのグローブを表示する場合にグローブを構成する頂点の座標値はどのように計算すればいいのでしょうか? 手首の関節の細かい動きなどを無視して下の図のように簡略化して考えると、グローブの位置はまず選手の肘との相対位置と方向で表す事ができそうです。 次に肘(ひじ)は肩、肩は腰、腰は膝、膝はかかと、かかとはリングというようにグローブから地面 (この場合リング)に向かって隣り合った位置と向きを考えると動いている物体の座標でも表現できそうです。
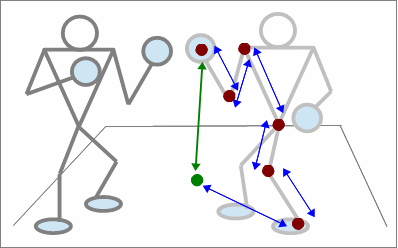
この場合のリングの中心 (図中の緑の点) のように色々な物体の基準となるような点を原点(0, 0, 0)とした座標系を考えて、 ワールド座標系と呼ぶことにします。 グローブはいくつかの頂点 (v) をつなぐ面を使って形を表すことが できますが、これらの頂点の1つ1つをワールド座標系で表し、 さらにコンピュータの画面上の2次元の座標に変換する必要があります。 これは非常に大変そうな計算に思えます。
これには非常にうまい方法があって、図中の青い矢印 で示している「肘と肩」のように隣り合った位置と向きは同次座標系の変換行列で表すことができます。 詳細は後から説明しますが、4x4の行列1つで隣り合った位置と向きが表現できます。 この行列(M)を乗算することで図中の緑の矢印に対応する 「手首→肘→肩→腰→膝→かかと→リング」 を1つの 4x4 行列で表すことができます。

上の式でカッコで括ったように、多段の座標変換に対応する行列を先に乗算しておくことができます。 頂点1つ当たり 1回の 4x4 行列との乗算で多段の座標変換ができます。 多くの頂点があっても計算量は最小限ですみます。
コンピュータの画面のドット (ピクセル) を表示するまでには、 さらにリングを撮影しているカメラに映るシーンへの「視点変換」、 遠く(画面奥)を小さく描く2次元の画像への「透視投影変換」、 コンピュータの画面のサイズに合わせるスクリーン変換を行なう必要があります。 これらの変換も4x4行列で行うことができるため、結局グローブのローカル座標系の 頂点 (vグローブ) が4x4行列との乗算でコンピュータの画面上の1点 (V画面) まで一撃で計算できます。

以上のように3次元グラフィックの基本としての 4x4 行列 (同次変換行列) の乗算が、 非常に重要でかつ便利なツールであることがお分かりいただけると思います。
行列とベクトルの乗算
行列x行列の乗算の前に、頂点座標(ベクトル) が 4x4行列との乗算で新しい座標に 変換される計算を見ておきましょう。 まず、上の式で出てきた V、M、v は次の形式のベクトルと行列を意味しています。
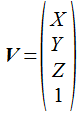 |
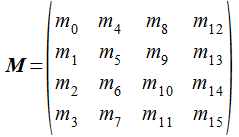 |
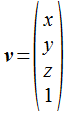 |
ベクトルV と v は、4行1列の列ベクトル(縦に並べたベクトル)として表します。 行列は16個の要素を持つ配列となっており、要素の添字はメモリに格納される順序を示します。 列優先で格納されていることになります。
頂点座標の変換は行列とベクトルを乗算するだけで計算できます。 頂点座標を列ベクトルとして表記する OpenGL では、行列とベクトル(頂点座標)の 乗算はベクトルの左から行列を乗算する形式となります。 そのため、後から乗算する行列ほど左側に置きます。
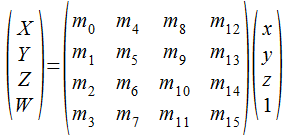
GPU (シェーダ) では整数同士の乗算とおなじく簡単で、行列とベクトルを乗算する コードを自分で書く必要はありませんが、実際に GPU 内部で行われるベクトルの各要素の計算は次のようになります。
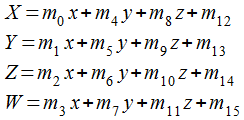
4x4行列と4要素のベクトルの乗算のCによるプログラムを示します。 まずベクトルは4要素を配列で持つ構造体を Vec4 という型名で宣言しています。
typedef struct {
float v[4];
} Vec4;
同様に4x4行列の16要素を配列で持つ構造体を Mat4 という型名で宣言しています。
typedef struct {
float m[16];
} Mat4;
4x4行列と4要素のベクトルの乗算は次のように乗算と加算を行うだけです。 実際にはこの計算はシェーダが行いますが、Cで書くと次のコードになります。
void mulMatrixVec(Vec4 *r, Mat4 *a, Vec4 *b)
{
float b0, b1, b2, b3;
b0 = b->v[ 0]; b1 = b->v[ 1]; b2 = b->v[ 2]; b3 = b->v[ 3];
r->v[ 0] = a->m[0] * b0 + a->m[4] * b1 + a->m[ 8]* b2 + a->m[12] * b3;
r->v[ 1] = a->m[1] * b0 + a->m[5] * b1 + a->m[ 9]* b2 + a->m[13] * b3;
r->v[ 2] = a->m[2] * b0 + a->m[6] * b1 + a->m[10]* b2 + a->m[14] * b3;
r->v[ 3] = a->m[3] * b0 + a->m[7] * b1 + a->m[11]* b2 + a->m[15] * b3;
}
平行移動と回転
同次変換行列は平行移動、回転といった座標変換を行うことができます。 平行移動や回転を行う行列の内容を見てみましょう。 平行移動や回転以外にも拡大縮小、せん断変形も可能ですが、 あまり使う機会はないと思います。
単位行列
さて、はじめに単位行列を紹介します。斜めに1が並ぶだけの行列で、 普通の掛け算の1のように単位行列を乗じても何も変化しません。 行列の初期化に使われます。
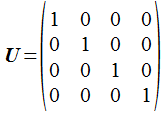
Cのコードは次のように書けます。全体をmemsetで 0 にした後、1にする部分 だけ上書きしています。「makeUnit(&m);」のように Mat4 型の変数のアドレスを 渡します。
void makeUnit(Mat4 *m)
{
memset(m, 0, sizeof(Mat4));
m->m[0] = m->m[5] = m->m[10]= m->m[15] = 1.0f;
}
平行移動
平行移動は単位行列のm12、m13、m14にx、y、z軸方向の移動量を設定するだけです。 したがって平行移動を行う同次変換行列は次のようになります。
 |
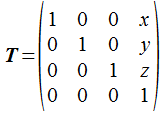 |
Cのコードは次のように書けます。移動だけの行列を作成する場合は単位行列に対してsetPosition を実行して下さい。
void setPosition(Mat4 *m, float x, float y, float z)
{
m->m[12] = x;
m->m[13] = y;
m->m[14] = z;
}
X軸回りの回転
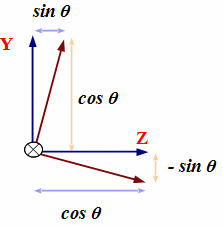
X軸回りの角度θの回転変換を行う行列はYとZの成分が変化し、次の形になります。 左側の図はX軸の根元から先に向かって見た場合のY軸とZ軸で、青い軸が回転前を示します。 回転の方向はX軸の先に向かって時計周りを正の方向とします。
 |
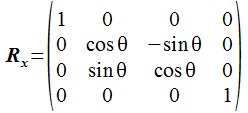 |
void setRotationX(Mat4 *m, float degree)
{
float rad = ((float)degree * M_PI / 180.0)
m->m[ 5] = cos(rad);
m->m[ 9] = - sin(rad);
m->m[ 6] = sin(rad);
m->m[10] = cos(rad);
}
Y軸回りの回転
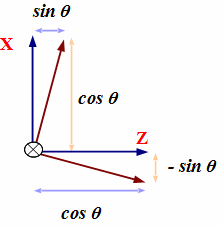
Y軸回りの角度θの回転変換を行う行列はXとZの成分が変化し、次の形になります。 左側の図はY軸の根元から先に向かって見た場合のX軸とZ軸で、青い軸が回転前を示します。 回転の方向はY軸の先に向かって時計周りを正の方向とします。
 |
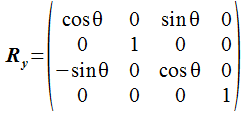 |
void setRotationY(Mat4 *m, float degree)
{
float rad = ((float)degree * M_PI / 180.0);
m->m[ 0] = cos(rad);
m->m[ 8] = sin(rad);
m->m[ 2] = - sin(rad);
m->m[10] = cos(rad);
}
Z軸回りの回転
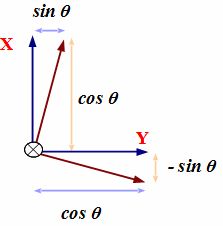
最後にZ軸回りの角度θの回転変換を行う行列はXとYの成分が変化し、次の形になります。 右側の図はZ軸の根元から先に向かって見た場合のX軸とY軸で、青い軸が回転前を示します。 回転の方向はZ軸の先に向かって時計周りを正の方向とします。
 |
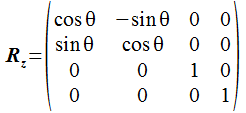 |
void setRotationZ(Mat4 *m, float degree)
{
float rad = ((float)degree * M_PI / 180.0);
m->m[ 0] = cos(rad);
m->m[ 4] = - sin(rad);
m->m[ 1] = sin(rad);
m->m[ 5] = cos(rad);
}
以上の同次変換行列T、Rx、Ry、Rz を乗算で組み合わせれば任意の座標変換が可能となります。乗算の順番は重要で 「Ry T : 平行移動してY軸回りに回転」と「 T Ry : Y軸回りに回転して平行移動」では結果は全く異なることに注意してください。 また、後の操作を示す行列が左側にあることにも注意してください。
行列同士の乗算
4x4行列と4x4行列の乗算は次のように計算します。 式が多いですが、機械的に乗算と加算を地味に行うだけです。
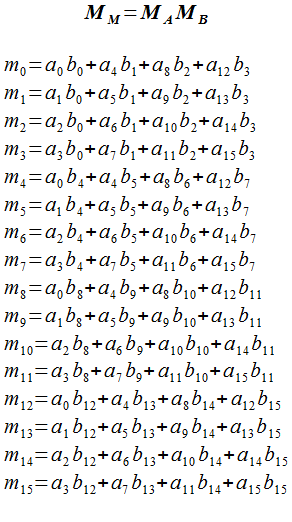
同じ計算を C で書くと以下のようになります。 行列Aと行列Bの要素をわざわざローカル変数に代入しているのは同じ配列の要素が4回ずつ参照されるため、 配列の参照よりローカル変数の参照の方が速いことを期待しています。 行列の乗算で乗算64回、加算48回の計算量となります。
void mulMatrix(Mat4 *r, Mat4 *a, Mat4 *b)
{
float a0, a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14, a15;
float b0, b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15;
a0 =a->m[ 0]; a1 =a->m[ 1]; a2 =a->m[ 2]; a3 =a->m[ 3];
a4 =a->m[ 4]; a5 =a->m[ 5]; a6 =a->m[ 6]; a7 =a->m[ 7];
a8 =a->m[ 8]; a9 =a->m[ 9]; a10=a->m[10]; a11=a->m[11];
a12=a->m[12]; a13=a->m[13]; a14=a->m[14]; a15=a->m[15];
b0 =b->m[ 0]; b1 =b->m[ 1]; b2 =b->m[ 2]; b3 =b->m[ 3];
b4 =b->m[ 4]; b5 =b->m[ 5]; b6 =b->m[ 6]; b7 =b->m[ 7];
b8 =b->m[ 8]; b9 =b->m[ 9]; b10=b->m[10]; b11=b->m[11];
b12=b->m[12]; b13=b->m[13]; b14=b->m[14]; b15=b->m[15];
r->m[ 0] = a0 * b0 + a4 * b1 + a8 * b2 + a12 * b3;
r->m[ 1] = a1 * b0 + a5 * b1 + a9 * b2 + a13 * b3;
r->m[ 2] = a2 * b0 + a6 * b1 + a10 * b2 + a14 * b3;
r->m[ 3] = a3 * b0 + a7 * b1 + a11 * b2 + a15 * b3;
r->m[ 4] = a0 * b4 + a4 * b5 + a8 * b6 + a12 * b7;
r->m[ 5] = a1 * b4 + a5 * b5 + a9 * b6 + a13 * b7;
r->m[ 6] = a2 * b4 + a6 * b5 + a10 * b6 + a14 * b7;
r->m[ 7] = a3 * b4 + a7 * b5 + a11 * b6 + a15 * b7;
r->m[ 8] = a0 * b8 + a4 * b9 + a8 * b10+ a12 * b11;
r->m[ 9] = a1 * b8 + a5 * b9 + a9 * b10+ a13 * b11;
r->m[10] = a2 * b8 + a6 * b9 + a10 * b10+ a14 * b11;
r->m[11] = a3 * b8 + a7 * b9 + a11 * b10+ a15 * b11;
r->m[12] = a0 * b12+ a4 * b13+ a8 * b14+ a12 * b15;
r->m[13] = a1 * b12+ a5 * b13+ a9 * b14+ a13 * b15;
r->m[14] = a2 * b12+ a6 * b13+ a10 * b14+ a14 * b15;
r->m[15] = a3 * b12+ a7 * b13+ a11 * b14+ a15 * b15;
}
平行移動と回転を行う同次変換行列を良く見ると、m[3]、m[7],m[11]は常にゼロ、 m[15]は常に1であることに気付きます。 これを利用すると平行移動と回転だけを行う場合には計算を省略する事ができて、 次のように乗算36回、加算27回となり、80%近く高速化できることが期待できます。
void mulMatrixFast(Mat4 *r, Mat4 *a, Mat4 *b)
{
float a0, a1, a2, a4, a5, a6, a8, a9, a10, a12, a13, a14;
float b0, b1, b2, b4, b5, b6, b8, b9, b10, b12, b13, b14;
a0 =a->m[ 0]; a1 =a->m[ 1]; a2 =a->m[ 2];
a4 =a->m[ 4]; a5 =a->m[ 5]; a6 =a->m[ 6];
a8 =a->m[ 8]; a9 =a->m[ 9]; a10=a->m[10];
a12=a->m[12]; a13=a->m[13]; a14=a->m[14];
b0 =b->m[ 0]; b1 =b->m[ 1]; b2 =b->m[ 2];
b4 =b->m[ 4]; b5 =b->m[ 5]; b6 =b->m[ 6];
b8 =b->m[ 8]; b9 =b->m[ 9]; b10=b->m[10];
b12=b->m[12]; b13=b->m[13]; b14=b->m[14];
r->m[ 0] = a0 * b0 + a4 * b1 + a8 * b2;
r->m[ 1] = a1 * b0 + a5 * b1 + a9 * b2;
r->m[ 2] = a2 * b0 + a6 * b1 + a10 * b2;
r->m[ 3] = 0.0;
r->m[ 4] = a0 * b4 + a4 * b5 + a8 * b6;
r->m[ 5] = a1 * b4 + a5 * b5 + a9 * b6;
r->m[ 6] = a2 * b4 + a6 * b5 + a10 * b6;
r->m[ 7] = 0.0;
r->m[ 8] = a0 * b8 + a4 * b9 + a8 * b10;
r->m[ 9] = a1 * b8 + a5 * b9 + a9 * b10;
r->m[10] = a2 * b8 + a6 * b9 + a10 * b10;
r->m[11] = 0.0;
r->m[12] = a0 * b12 + a4 * b13+ a8 * b14 + a12;
r->m[13] = a1 * b12 + a5 * b13+ a9 * b14 + a13;
r->m[14] = a2 * b12 + a6 * b13+ a10 * b14 + a14;
r->m[15] = 1.0;
}
モデルビュー行列と透視投影変換行列
3次元のコンピュータグラフィックスで行う計算を次のようにまとめます。 座標系の頂点座標 v と ワールド座標系への変換行列 (Mworld)、 視点座標系への変換行列 (Meye)、 2次元への透視投影変換を行う透視投影変換行列 (Mproj) の乗算です。
これまでの OpenGL (の固定機能) では、ワールド座標系への変換行列と 視点座標系への変換行列の積 (MeyeMworld) をモデルビュー行列と呼んでローカル座標系の頂点座標から視点座標系への 変換に使っていました。 投影変換行列とモデルビュー行列を区別して使う必要がありました。
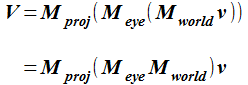
シェーダを使う OpenGL では、行列を好きなように分けて利用できます。 ここで、物体がその場で回転する事を考えます。 物体を構成する頂点の座標はローカル座標系で定義されているので、 ローカル座標系の頂点を行列 Mrotateで回転したものを順次「ワールド座標系→視点座標系→透視投影変換」する必要があります。 モデルビュー行列として考えると (Meye Mworld Mrotate ) としてまとめることになります。
描画の度に回転させてアニメーションとするには Mrotate を頂点に最初に乗算する事で回転角を変化させてモデルビュー行列を 毎フレーム計算する必要があります。 今回は視点 (カメラ)は移動しないため、Meye は固定になっています。 したがって、 変化しない投影変換行列とビュー行列、再計算して毎フレーム渡す必要のあるモデル行列の2つに分けることにします。
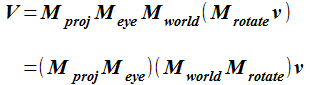
バーテックスシェーダの作り方と利用の仕方によりますが、 すべてアプリケーション側で乗算して1つの行列だけを渡すこともできます。 あるいは次のように変化するMrotateだけを別に渡す形式も可能です。 この辺はアプリケーションの内容とCPUとGPUの負荷のバランスの問題になります。 もしWebGLの場合ならば、速度を考えるとJavaScriptで行列の乗算する選択はなく、 極力シェーダ側で計算することになります。
頂点シェーダにおける座標変換
回転する物体を表示するためには、物体の頂点が画面上でどのような位置になるかを常に計算する必要があります。 頂点の座標変換は専用のシェーダ、バーテックスシェーダで行います。 前回のサンプルの三角形のデータが使えるように、各頂点は頂点座標 (x、y、z) と テクスチャ座標 (u,v) を情報として持っているものとします。
前回のバーテックスシェーダと異なっているのは uFrame の代わりに uVpMatrix と uModelMatrix をユニフォーム変数として渡せるようになっている ことと、頂点座標に uVpMatrix と uModelMatrix を掛けていることです。 uVpMatrix には 投影変換行列とビュー行列の積(Mproj Meye) を、 uModelMatrix には頂点を回転した後、 ワールド座標系に座標変換するモデル行列 (Mworld Mrotate )を渡します。
赤い部分が 前回のバーテックスシェーダ との違いです。 行列を2つ (uVpMatrix と uModelMatrix) 渡して、頂点座標と乗算しています。 フラグメントシェーダは前回と同じです。
attribute vec3 aPosition; attribute vec2 aTex; varying vec2 vTex; uniform mat4 uVpMatrix; uniform mat4 uModelMatrix; void main(void) { vTex = aTex; gl_Position = uVpMatrix * uModelMatrix * vec4(aPosition, 1.0); }
透視投影変換行列
3次元から2次元に変換する行列(透視投影変換行列)も次のように 4x4行列で表せます。 ビューボリュームのサイズのパラメータとして、n は視点に近い側の面までの距離、f は視点から遠い側の面までの距離、 r は nにおける右端の x 座標、l は n における左端の x 座標、t は n における上端の y 座標、 b は n における下端の y 座標を示します。
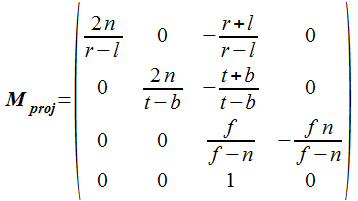
表示範囲が上下、左右対称の場合は次のようになります。w は表示領域の幅、h は表示領域の高さを示します。
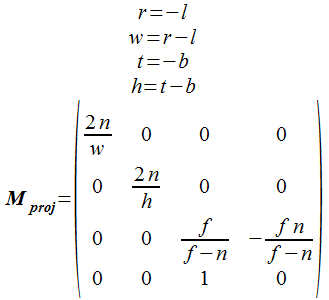
近面 (near) と画面の幅や高さで表すのではなく、視野角と画面の縦横比 (アスペクト比) で透視投影変換行列を表すこともできます。 次のコードは横方向の視野角(hfov) と横/縦 (例えば 1920/1080 = 1.778) の比率で表示範囲を指定して変換行列を求めます。 近面、遠面ともにZ値ではなく距離(つまり正の値)で指定します。横方向の視野角(hfov) は通常は90度、 ちょっとズーム気味で53度が使いやすい値です。 視野角90度のとき視点から物体までの距離の2倍が見える範囲、視野角53度のとき 視点から物体までの距離と同じ大きさが水平方向の見える範囲となります。
//---------------------------------------------------------------------
// 射影行列を近面、遠面、視野角、アスペクト比で指定
//---------------------------------------------------------------------
void makeProjectionMatrix(Mat4 *m, float n, float f, float hfov, float r)
{
float w = 1.0f / tan(hfov * 0.5f * M_PI / 180);
float h = w * r;
float q = 1.0f / (f - n);
m->m[0] = w;
m->m[5] = h;
m->m[10]= -(f + n) * q;
m->m[11]= -1.0f;
m->m[14]= -2.0f * f * n * q;
m->m[1] = m->m[2] = m->m[3] = m->m[4] = m->m[6] = m->m[7]
= m->m[8] = m->m[9] = m->m[12] = m->m[13] = m->m[15] = 0.0f;
}
サンプルコード
今回のサンプルは、三角形をその場で20秒間 X 軸を中心に回転させます。 main 関数は初期化した後、描画を1200回(20秒間)繰り返しています。 三角形の頂点座標をその場で回転させて、視点座標系に移動して表示します。
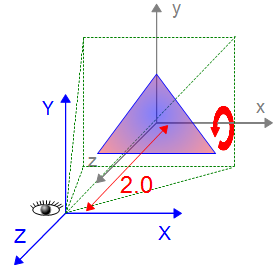
main 関数の 前回との違いを赤で示していますが、 2次元への透視投影変換行列を g_sp.VpMatrix に設定して、 ワールド座標系から視点座標系への変換行列(距離 2.0 だけ後ろにずらす) を viewMat に設定しています。 viewMat に対して透視投影変換行列を左から乗算して g_sp.VpMatrix に格納します。glUniformMatrix4fv でシェーダのユニフォーム変数 uVpMatrix に渡します。この値はサンプルの実行中変化しません。
三角形の回転は、三角形の頂点座標を三角形の頂点座標を定義したローカル座標系で 回転 (rotMatを乗算) させて、ワールド座標系にモデル行列で座標変換 (実際には単位行列なので何もしない) することで実現(modelMat = modelMat * rotMat)しています。 描画ループ内で繰り返しモデル行列 (modelMat) に回転行列 (rotMat) を掛けることで回転させています。
int main ( int argc, char *argv[] )
{
unsigned int frames = 0;
int res;
Mat4 viewMat;
Mat4 rotMat;
Mat4 modelMat;
float aspect;
bcm_host_init();
res = WinCreate(&g_sc);
if (!res) return 0;
res = SurfaceCreate(&g_sc);
if (!res) return 0;
res = InitShaders(&g_program, vShaderSrc, fShaderSrc);
if (!res) return 0;
createBuffer();
glUseProgram(g_program);
g_sp.aPosition = glGetAttribLocation(g_program, "aPosition");
g_sp.aTex = glGetAttribLocation(g_program, "aTex");
// シェーダのユニフォーム変数の番号を記録
g_sp.uVpMatrix = glGetUniformLocation(g_program, "uVpMatrix");
g_sp.uModelMatrix = glGetUniformLocation(g_program, "uModelMatrix");
// 画面のアスペクト比を求めて透視投影変換行列を作成
aspect = (float)g_sc.width / (float)g_sc.height;
makeProjectionMatrix(&g_sp.VpMatrix, 1, 1000, 53, aspect);
// ワールド座標系から視点 (0, 0, 2) への変換行列(ビュー行列)を作成
makeUnit(&viewMat);
setPosition(&viewMat, 0, 0, -2);
// 透視投影変換行列とビュー行列を乗算
mulMatrix(&g_sp.VpMatrix, &g_sp.VpMatrix, &viewMat);
// バーテックスシェーダに渡す
glUniformMatrix4fv(g_sp.uVpMatrix, 1, GL_FALSE, g_sp.VpMatrix.m);
// 三角形のためのワールド座標系への変換行列(モデル行列)を作成 (何もしない単位行列)
makeUnit(&modelMat);
glUniformMatrix4fv(g_sp.uModelMatrix, 1, GL_FALSE, modelMat.m);
// X軸回りに0.5度回転させる行列を作成
makeUnit(&rotMat);
setRotationX(&rotMat, 0.5); /* 30 degree/sec */
// 深度テストを有効にする
glEnable(GL_DEPTH_TEST);
glClearColor(0.0f, 0.2f, 0.4f, 1.0f);
/* 1200frame / 60fps = 20sec */
while(frames < 1200) {
glViewport(0, 0, g_sc.width, g_sc.height);
// 深度バッファも消去
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// モデル行列を0.5度X軸回転させて更新
mulMatrix(&modelMat, &modelMat, &rotMat);
// バーテックスシェーダに渡す
glUniformMatrix4fv(g_sp.uModelMatrix, 1, GL_FALSE, modelMat.m);
Draw();
eglSwapBuffers(g_sc.display, g_sc.surface);
frames++;
}
return 0;
}
ソースのダウンロードと使い方
今回の三角形が X軸まわりに回転するだけのサンプルのソースです。
- Jessie 以前向け: triangel02.tar.gz (8.4KB)
- Raspbian Stretch 向け: triangel02a.tar.gz (10KB) (2017/12/24)

triangle.c が今回のソース全体、triangle はコンパイルした実行ファイル、build はコンパイル用のシェルスクリプトです。
jun@raspberrypi ~/triangle02a $ ls -lt -rwxr-xr-x 1 pi pi 14968 Dec 7 16:11 triangle -rw-r--r-- 1 pi pi 10382 Dec 7 16:11 triangle.c -rwxr-xr-x 1 pi pi 211 Dec 7 16:09 build
公式OSの Raspbian の場合、pi ユーザ(または video グループ権限を持つユーザ) で以下のようにファイルを解凍して、コンパイル、実行できます。20秒間動作して終了します。
$ tar zxf triangle02a.tar.gz $ cd triangle02a $ ./build $ ./triangle
シェーディングを行なっていない (照明がない) ため、前後関係が分かり難いですが、最初に三角形の底辺が小さくなる (遠ざかる) ため、X軸の正の方向に回転していることが確認できます。
